Aula 06 - Portas Lógica Booleanas por Diodos e Resistores

 Tabela Verdade

Utilizando um simples arranjo de resistores e diodos é possível construir portas lógicas, esse arranjo tem o nome de lógica resistor-diodo (RDL).

Uma porta NOT, AND  ou OR pode ser compreendido observando-se a tabela verdade desta função, na figura 1.

Porta Lógica NOT com resistor e transistor lógico: Uma porta RTL NOT com 1 entradas consiste em um transistores com todos o emissor conectado a um terra comum e todos o coletor interligado através de um resistor de coletor Rc para uma tensão de alimentação Vcc. 

As tensões de entradas Vi representando nível lógico é aplicado na base através de resistores R que provoca a condução do transistor mandando nível logico zero na saída.

Porta Lógica AND com diodos e resistores: Para conseguirmos sintetizar essa lógica em um circuito vamos utilizar a topologia apresentada na figura 2. Como pode ser evidenciado na tabela verdade da função lógica a única condição em que o circuito terá um sinal alto na saída ocorre quando as duas entradas, A e B, também estão em nível alto, para qualquer outra combinação de sinais a saída AB será zero, deve-se tomar cuidado que o nível baixo é compreendido, neste caso, como sendo a conexão da respectiva entrada a referência. Quando nesta porta as duas entradas estão lógico alto nível ("1"), os dois díodos são polarizados no sentido inverso e não conduz corrente e, portanto, a saída é uma lógica alta ("1")

Se uma das entradas é baixo, então a saída será baixo ("0"), então a corrente fluirá através da resistência e diodo cujo cátodo estão ligado à terra. Assim, o ânodo do díodo (saída) será baixo.

Porta Lógica OR (Porta OU) com diodos e resistores: A função lógica OR (função OU) diz que se ao menos um dos operandos  for verdadeiro o resultado será verdadeiro. Operação ou está relacionada a operação de união da teoria dos conjuntos e normalmente adota-se o símbolo + para representar a operação da Porta OR. Definindo 1 como Verdadeiro e 0 a Falso, a expressão A+B representa um porta Lógica com duas entradas (A e B), como pode ser visto na figura. Um forma de mapear as possibilidades de operação de uma função lógica é através da tabela verdade, na Tabela 1 estão representados os valores que a operação A+B pode assumir.

Os diodo D1 e o D2 são as entradas da porta ou. Quando o diodo está diretamente polarizado a tensão da porta A ou B surge sobre a resistência Y. Nesse caso o resistor R1 (resistor pull-down) garante o nível lógico zero na situação de nenhum dos diodos estar conduzindo.
Neste tipo de circuito, se uma ou ambas as entradas são um "1" (5 volts ), vai fluir corrente através de um ou ambos os diodos . Esta corrente vai passar através da resistência , que por sua vez terá uma tensão entre os seus terminais alta e dará um nível lógico "1" na saída.
Com este arranjo você terá "0" na saída somente quando ambas as entradas são baixos ("0"). Assim, nenhum díodo conduz, nenhuma corrente flui através do resistor e não há nenhuma queda na tensão. Como resultado, a tensão no Vout é zero (0 volts ).

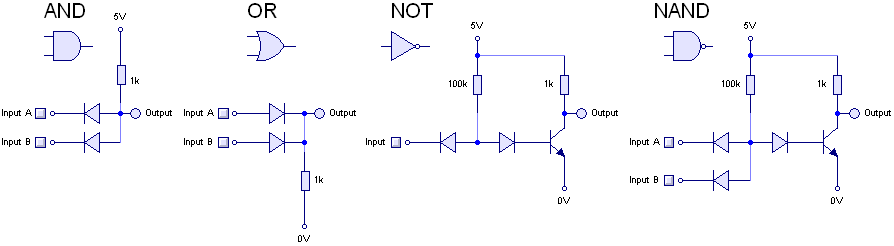
Aula 05 - Portas Lógicas Booleanas por chave

Os relés executam um controle de operação em uma máquina através de uma função lógica. As funções lógicas fundamentais que conhecemos são as operações “E” (AND), “OU” (OR), e a “NEGADO” (NOT). Combinando as portas lógicas corretamente, podemos executar qualquer função lógica desejada. Em cada caso, a porta lógica é projetada para prover um valor específico em sua saída, baseado nos valores das entradas. Tanto para as entradas quanto para as saídas temos dois valores específicos (valores binários): o 0 (zero) e o 1 (um). Para o controle industrial, tratamos o 0 (zero) como OFF (desligado) e o 1(um) com ON (ligado). Em conjunto com as portas lógicas utilizamos uma tabela, a que chamamos de Tabela Verdade, para cada um dos circuitos que projetamos. O objetivo é representar todas as combinações possíveis nas entradas do circuito e suas respectivas saídas.

Porta lógica “E” (and) - A porta lógica “E” retorna um valor de saída em 1 quando todas as suas entradas estiverem com o valor lógico 1. A figura ilustra a operação de uma porta lógica “E”, com a respectiva Tabela Verdade, que expressa a operação lógica do sistema. Se as entradas X1 e X2 estiverem fechadas, a lâmpada Y estará ligada. A porta “E” é utilizada quando queremos que duas ou mais ações sejam completadas, para que possamos dar continuidade ao processo.

Porta Lógica “OU” (or) - A porta lógica “OU” retorna um valor de saída em 1 quando qualquer uma das entradas estiver com o valor lógico 1. A figura ilustra a operação de uma porta lógica “OU, com a respectiva Tabela Verdade, que expressa a operação lógica do sistema. Se a entrada X1 ou a entrada X2 estiver fechada, a lâmpada Y estará ligada. A porta “OU” é utilizada quando queremos monitorar um sistema em que apenas uma das ações seja completada, para que possamos dar continuidade ao processo.

Porta lógica “Negada” (not) - A porta lógica “NEGADA” tem apenas uma entrada e retorna na saída o valor invertido; ou seja, se a entrada estiver em 1, então a saída terá valor lógico de 0 (zero) e vice-versa.

A figura 35 ilustra a operação de uma porta lógica “NEGADA”, com a respectiva Tabela Verdade, que expressa a operação lógica do sistema. Colocamos a entrada X1 em paralelo com a saída Y. Nesse caso, a corrente vai no sentido da menor resistência; ou seja, se a entrada X1 estiver aberta, a corrente passará pela saída Y e, caso a entrada X1 esteja fechada, então a saída Y não acionará.

Aula 04 - Lógica de Boole

Portas lógicas ou circuitos lógicos, são dispositivos que operam um ou mais sinais lógicos de entrada para produzir uma e somente uma saída, dependente da função implementada no circuito. São geralmente usadas em circuitos eletrônicos, por causa das situações que os sinais deste tipo de circuito podem apresentar: presença de sinal, ou "1"; e ausência de sinal, ou "0". 

As situações "Mentirosas" e "Falsa" são estudadas na Lógica Matemática ou Lógica de Boole; origem do nome destas portas. O comportamento das portas lógicas é conhecido pela tabela verdade que apresenta os estados lógicos das entradas e das saídas. 

George Boole era um estudioso de operações matemáticas de forma diferente, separava todos os símbolos das coisas sobre as quais eles operavam, com o intuito de criar um sistema simples e totalmente simbólico. Surge assim a lógica matemática. Mas, como a Lógica de Boole (ou lógica booleana) utiliza um sistema numérico binário, na época de sua descoberta não foi utilizada. Com o surgimento do computador, a utilização do sistema binário tornou-se indispensável e, obviamente, a lógica de Boole passou a ter aplicação prática. 

É possível construir proposições lógicas a partir de proposições já existentes. Este processo é conhecido por Composição de Proposições. 

Suponha que tenhamos duas proposições, 1. A = "Maria tem 23 anos" 2. B = "Maria é menor".

Pela legislação corrente de um país fictício, uma pessoa é considerada de menor idade caso tenha menos que 18 anos, o que faz com que a proposição B seja F, na interpretação da proposição A ser V. 

Vamos a alguns exemplos: 

1. "Maria não tem 23 anos" (nãoA) 

2. "Maria não é menor"(não(B)) 

3. "Maria tem 23 anos" e "Maria é menor" (A e B) 

4. "Maria tem 23 anos" ou "Maria é menor" (A ou B) 

5. "Maria não tem 23 anos" e "Maria é menor" (não(A) e B) 

6. "Maria não tem 23 anos" ou "Maria é menor" (não(A) ou B) 

7. "Maria tem 23 anos" ou "Maria não é menor" (A ou não(B)) 

8. "Maria tem 23 anos" e "Maria não é menor" (A e não(B)) 

9. Se "Maria tem 23 anos" então "Maria é menor" (A => B) 

10. Se "Maria não tem 23 anos" então "Maria é menor" (não(A) => B) 

11. "Maria não tem 23 anos" e "Maria é menor" (não(A) e B) 

12. "Maria tem 18 anos" é equivalente a "Maria não é menor" (C <=> não(B)) 

Note que, para compor proposições usou-se os símbolos não (negação), e (conjunção), ou (disjunção), => (implicação) e, finalmente, <=> (equivalência). São os chamados conectivos lógicos. Note, também, que usou-se um símbolo para representar uma proposição: C representa a proposição Maria tem 18 anos. Assim, não(B) representa Maria não é menor, uma vez que B representa Maria é menor.
Esposa do analista de sistemas: - Zé, vai na padaria e traz 5 pães. Se tiver ovos, traz 6.
Ele voltou com 6 pães e disse: - Tinha ovos !

Aula 03 - Sistema de Numeração Hexadecimal

O sistema hexadecimal é um sistema de numeração posicional que representa os números em base 16, portanto, emprega 16 símbolos. Devido ao sistema decimal geralmente usado para a numeração apenas dispor de dez símbolos, deve-se incluir seis letras adicionais para completar o sistema. O conjunto de símbolos fica, portanto, assim: H = {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}. Note que A=10, B=11, C=12, D=13. E=14, F=15. 

O sistema hexadecimal é utilizado para expressar números binários utilizando poucos dígitos, uma vez que utiliza um dígito para representar quatro dígitos binários. Tal como nos restantes sistemas numéricos, os números em hexadecimal podem ser representados em decimal aplicando o método da soma dos pesos.

Assim como nos outros sistemas numéricos, após o uso de todos os dígitos hexadecimais, se inicia a repetição com a adição de outro dígito: (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21, 22…).

Pode parecer pouca a diferença para os números decimais, porem esses 6 dígitos a mais fazem muita diferença. Por exemplo, com dois dígitos, em decimal, é possível fazer 100 combinações diferentes. Em hexadecimal, esse número sobe para 256. 

A Conversão de Binário para Hexadecimal é realizada ao agrupar os dígitos binários quatro a quatro, a partir da vírgula binária, em ambas as direções e substituir cada grupo pelo seu equivalente hexadecimal. 10011111100,1101001010102 = 4FC,D2A16 Já a conversão Hexadecimal para Binário devemos substituir cada dígito hexadecimal pelo binário equivalente de quatro dígitos. DEA16 = 1101111010102.

Aula 02 - Sistema de Numeração Binária

O sistema decimal é muito usado no cotidiano, pois nos oferece uma forma mais simples de manipular os números em determinadas situações matemáticas, é composto por dez números: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

O uso da Matemática em situações diversas não diz respeito somente ao homem, os computadores utilizam números para efetuar cálculos complexos com uma maior rapidez e praticidade. O sistema binário é usado pelos computadores é e constituído de dois dígitos o 0 e o 1. A combinação desses dígitos leva o computador a criar várias informações: letras, palavras, textos, cálculos.

A criação do sistema de numeração binária é atribuída ao matemático alemão Leibniz.

O sistema binário ou base 2, é um sistema de numeração posicional em que todas as quantidades se representam com base em dois números, com o que se dispõe das cifras: zero e um (0 e 1). 

Os computadores digitais trabalham internamente com dois níveis de tensão, pelo que o seu sistema de numeração natural é o sistema binário (aceso, apagado). Com efeito, num sistema simples como este é possível simplificar o cálculo, com o auxílio da lógica booleana. Em computação, chama-se um dígito binário (0 ou 1) de bit, que vem do inglês Binary Digit. Um agrupamento de 8 bits corresponde a um byte (Binary Term). Um agrupamento de 4 bits é chamado de nibble. 

Convertendo 9 (Base 10) para binário temos: 1001 (Base 02). O número binário será formado agrupando o último resultado seguido dos restos das divisões anteriores.

E como realizamos a conversão contrária? Como passamos um elemento representado no sistema de numeração binária para o sistema de numeração decimal ?

Quando convertemos do decimal para o binário nós dividimos, e quando fazemos o processo contrário, ou seja, binário para o decimal nós elevamos a potência. Segue abaixo: Transformando 1100 (BASE 02) para sistema de numeração decimal.

As bases para elevar as potências seguem a seguinte ordem: 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2 e 1.

Aula 01 - Aritimética - Sistema de Numeração Decimal

O sistema de numeração que usamos nos dias atuais demorou milhares de anos para ser organizado. Não foi criado por uma pessoa ou um único povo, mas é resultado de ideias de muitos povos. O sistema de numeração indo-arábica, como ficou conhecido, surgiu na Ásia, no vale do rio Indo, onde hoje é o Paquistão. Os árabes, durante suas invasões, aprenderam com os hindus e depois levaram para a Europa.

No século IX, viveu um matemático e astrônomo árabe chamado Mohammed ibm-Musa al-Khowarizmi. Ele escreveu o livro Sobre a Arte Hindu de Calcular, no qual explicava com detalhes o sistema numeral hindu. Traduzido para o latim, esse livro foi muito utilizado na Europa por quem queria aprender a nova numeração, que ficou conhecida como "a numeração de al-Khowarizmi". Com o tempo, o nome do matemático foi modificado para Algorismi. Em português, deu origem à palavra algarismo. 

A genialidade da numeração indo-arábica está em sua praticidade. Veja só:

Só são necessários 10 símbolos (ou algarismos): 1, 2, 3, 4, 5, 6, 7, 8, 9 e 0. 

Contamos de 10 em 10, ou seja, formando grupos de 10. 

O valor de cada algarismo varia de acordo com a posição que ocupa no número (o 2, no 12, vale 2, mas no 27 vale 20. No 237, vale 200). 

Temos um símbolo para representar o "nada". A ausência de objetos é representada pelo zero.

No princípio, os números ajudaram o homem a quantificar seu rebanho, sua comida e a medir o tamanho de suas terras. Até esse momento, não havia a necessidade da utilização do zero, por isso, os sistemas de numeração primitivos, como romano, grego, chinês e egípcio, foram criados sem a presença de um símbolo que representasse a ausência de quantidade.

Foram os babilônios os primeiros a criarem um símbolo para a posição de “vazio” intermediária, como no número 103 (o zero é a casa vazia). Coube aos hindus, no entanto, a criação do símbolo que designava a quantidade nula. Quando os hindus desenvolveram o sistema numérico no qual o valor do algarismo variava de acordo com a posição, encontraram um problema de difícil solução: como identificar a ausência de um valor? Por exemplo: no número 347, o 3 valia 300 (centena), o 4 valia 40 (dezena) e o 7 representava a unidade. Mas como escrever 301? Que símbolo indicaria a ausência da dezena? Para resolver o problema, os hindus criaram o zero.

Com a criação do zero, o sistema de numeração indo-arábico (indiano e árabe) foi capaz de incorporar características já existentes em outros sistemas e basear sua contagem de dez em dez, assim como usamos hoje!

O formato dos caracteres numéricos que usamos foi traçado de modo que cada símbolo tenha uma quantidade de ângulos correspondente ao número que ele mesmo designa. Logo, o numeral “1” tem um ângulo; o "2" tem dois ângulos; o "3" tem três ângulos e, assim, sucessivamente. Apenas o "0" não tem ângulo nenhum.
Sistema Decimal é o sistema de numeração adotado em todas as operações matemáticas cotidianas. Este sistema é de base 10, no qual todos os múltiplos e submúltiplos são expressos como potência de 10.
Para entender o sistema, basta decompor qualquer número inteiro em potência de base DEZ.

Fonte: << http://www.klickeducacao.com.br >>

Aula 00 - Sistema de Numeração dos Romanos

De todas as civilizações da Antigüidade, a dos romanos foi sem dúvida a mais importante. Seu centro era a cidade de Roma. Desde sua fundação, em 753 a.C., até ser ocupada por povos estrangeiros em 476 d.C., seus habitantes enfrentaram um número incalculável de guerras de todos os tipos. Inicialmente, para se defenderem dos ataques de povos vizinhos; mais tarde nas campanhas de conquistas de novos territórios.

Foi assim que, pouco a pouco, os romanos foram conquistando a península Itálica e o restante da Europa, além de uma parte da Ásia e o norte de África.

Apesar de a maioria da população viver na miséria, em Roma havia luxo e muita riqueza, usufruídas por uma minoria rica e poderosa. Roupas luxuosas, comidas finas e festas grandiosas faziam parte do dia-a-dia da elite romana.

Foi nesta Roma de miséria e luxo que se desenvolveu e aperfeiçoou o número concreto, que vinha sendo usado desde a época das cavernas. 

Os romanos não inventaram símbolos novos para representar os números; usaram as próprias letras do alfabeto. I, V, X, L, C, D, M.

O sistema de numeração romano baseava-se em sete números-chave: I tinha o valor 1. V valia 5. X representava 10 unidades. L indicava 50 unidades. C valia 100. D valia 500. M valia 1.000.

Quando apareciam vários números iguais juntos, os romanos somavam os seus valores. II = 1 + 1 = 2; XX = 10 + 10 = 20.

Quando dois números diferentes vinham juntos, e o menor vinha antes do maior, subtraíam os seus valores. IV = 4 porque 5 - 1 = 4; IX = 9 porque 10 – 1 = 9; XC = 90 porque 100 – 10 = 90

Mas se o número maior vinha antes do menor, eles somavam os seus valores.

VI = 6 porque 5 + 1 = 6; XXV = 25 porque 20 + 5 = 25; XXXVI = 36 porque 30 + 5 + 1 = 36; LX = 60 porque 50 + 10 = 60. 

Ao lermos o cartaz, ficamos sabendo que o exército de Roma fez numa certa época MCDV prisioneiros de guerra. Para ler um número como MCDV, veja os cálculos que os romanos faziam: Em primeiro lugar buscavam a letra de maior valor. M = 1.000; como antes de M não tinha nenhuma letra, buscavam a segunda letra de maior valor; D = 500 ; Depois tiravam de D o valor da letra que vem antes. D – C = 500 – 100 = 400. Somavam 400 ao valor de M, porque CD está depois e M. M + CD = 1.000 + 400 = 1.400. Sobrava apenas o V. Então: MCDV = 1.400 + 5= 1.405

Os números criados pelos romanos foram relacionados a letras, diferente de outros povos que criaram símbolos na representação numérica de algarismos. Os números romanos utilizavam as letras I, V, X, L, C, D, M na representação dos seguintes valores: 1, 5, 10, 50, 100, 500, 1000 respectivamente. O interessante desse sistema de numeração é a ausência de uma letra relacionada ao número zero. Mas ao criar esse sistema de numeração, os romanos não estavam interessados na realização de cálculos. Eles simplesmente queriam números representativos para a determinação de quantidades, como contar objetos, animais, armas e etc. A representação numérica adotada pelos romanos foi durante muitos séculos a mais utilizada por toda a Europa.

Com o desenvolvimento da expansão comercial, a utilização de cálculos matemáticos tornou-se uma questão primordial. Foi nesse momento que os números romanos foram questionados em razão da ausência do zero e da representação de valores por letras. Essas características principais do sistema de numeração dos romanos dificultavam o desenvolvimento de técnicas matemáticas eficazes. Alguns estudiosos romanos tentaram relacionar o sistema numérico com a utilização do ábaco, mas os meios operantes requisitavam conhecimentos complexos.

O algarismo zero, ausente no sistema de numeração dos romanos, fora descoberto pelo povo hindu, bem como um novo sistema de numeração semelhante ao utilizado atualmente. Esse sistema consistia em uma base decimal (dez algarismos) que ordenados entre si formavam e representavam qualquer número. O sistema criado pelos hindus fora divulgado por toda a Europa pelos árabes, passando a ser conhecido como sistema de numeração indo-arábico. Esses números contribuíram de forma incessante na modernização dos cálculos matemáticos, em razão de sua praticidade simbólica e representação de quantidades.

Atualmente, os números romanos são utilizados na representação de nomes de papas e reis, de séculos, nomes de ruas, marcações de relógios, capítulos de livros etc.